Different methods of design of RCC
1.Working Stress Method
2.Limit State Method
3.Ultimate Load Method
4.Probabilistic Method of Design
Limit state method of design
- The object of the design based on the limit state concept is to achieve an acceptable probability, that a structure will not become unsuitable in it’s lifetime for the use for which it is intended,i.e. It will not reach a limit state
- A structure with appropriate degree of reliability should be able to withstand safely.
- All loads, that are reliable to act on it throughout it’s life and it should also satisfy the subs ability requirements, such as limitations on deflection and cracking.
- It should also be able to maintain the required structural integrity, during and after accident, such as fires, explosion & local failure.i.e. limit sate must be consider in design to ensure an adequate degree of safety and serviceability
- The most important of these limit states, which must be examine in design are as follows Limit state of collapse
- Flexure
- Compression
- Shear
- Torsion
This state corresponds to the maximum load carrying capacity.Types of reinforced concrete beams
a)Singly reinforced beam
b)Doubly reinforced beam
c)Singly or Doubly reinforced flanged beams
Singly reinforced beam
In singly reinforced simply supported beams or slabs reinforcing steel bars are placed near the bottom of the beam or slabs where they are most effective in resisting the tensile stresses.





x = Depth of Neutral axis
b = breadth of section
d = effective depth of section
The depth of neutral axis can be obtained by considering the equilibrium of the normal forces , that is,
Resultant force of compression = average stress X area
= 0.36 fck bx
Resultant force of tension = 0.87 fy At
Force of compression should be equal to force of tension,
0.36 fck bx = 0.87 fy At
The distance between the lines of action of two forces C & T is called the lever arm and is denoted by z.
Lever arm z = d – 0.42 x
z = d – 0.42
z = d –(fy At/fck b)
Moment of resistance with respect to concrete = compressive force x lever arm
= 0.36 fck b x z
Moment of resistance with respect to steel = tensile force x lever arm
= 0.87 fy At z
Maximum depth of neutral axis
- A compression failure is brittle failure.
- The maximum depth of neutral axis is limited to ensure that tensile steel will reach its yield stress before concrete fails in compression, thus a brittle failure is avoided.
- The limiting values of the depth of neutral axis xm for different grades of steel from strain diagram.


Limiting value of tension steel and moment of resistance
- Since the maximum depth of neutral axis is limited, the maximum value of moment of resistance is also limited.
- Mlim with respect to concrete = 0.36 fck b x z
- = 0.36 fck b xm (d – 0.42 xm)
- Mlim with respect to steel = 0.87 fck At (d – 0.42 xm)

Design of a section
Design of rectangular beam to resist a bending moment equal to 45 kNm using (i) M15 mix and mild steel.
The beam will be designed so that under the applied moment both materials reach their maximum stresses.
Assume ratio of overall depth to breadth of the beam equal to 2.
Breadth of the beam = b
Overall depth of beam = D
therefore , D/b = 2
For a balanced design,
Factored BM = moment of resistance with respect to concrete
= moment of resistance with respect to steel
= load factor X B.M
= 1.5 X 45
= 67.5 kNm
For balanced section,
Moment of resistance Mu = 0.36 fck b xm(d - 0.42 xm)
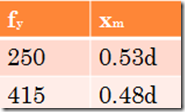
Grade for mild steel is Fe250
For Fe250 steel,
xm = 0.53d
Mu = 0.36 fck b (0.53 d) (1 – 0.42 X 0.53) d
= 2.22bd
Since D/b =2 or, d/b = 2 or, b=d/2
Mu = 1.11 d
Mu = 67.5 X 10 Nmm
d=394 mm and b= 200mm
Adopt D = 450 mm , b = 250 mm ,d = 415mm

=(0.85x250x415)/250
= 353 mm
353 mm < 962 mm
In beams the diameter of main reinforced bars is usually
selected between 12 mm and 25 mm.
Provide 2-20mm and 1-22mm bars giving total area
= 6.28 + 3.80
= 10.08 cm > 9.62 cm



supper
ReplyDeletegoooddd
ReplyDeleteHello, i just opted with a subscriber list upon a few website marketing website
ReplyDeletenow I actually retain receiving a great number of electronic mails at my mail that it essentially damaged
that email address. Plus the unsubscbribe url doesn't work frequently. Is it possible to as being a blog writer suggest myself how to handle it, due to the fact I might enjoy and keep that email.
Stop by my site - Treatment Of Genital Warts
Why My spouse and i i never thought of this?
ReplyDeleteHere is my page ... Female Car Insurance
Simply want to say your article is as astounding.
ReplyDeleteThe clarity in your post is simply cool and i could assume you're an expert on this subject. Well with your permission let me to grab your feed to keep up to date with forthcoming post. Thanks a million and please continue the enjoyable work.
my website ... San Diego video specialists
Keep this going please, great job!
ReplyDeleteHere is my web blog :: www.steveblisslaw.com
We sympathize with this subject even before "Singly reinforced beam(Limit state method of design)".
ReplyDeleteWe are in OC|an Orange County real estate.
Also visit my page :: good Orange County real estate agent
Great post shared here.Thanks for sharing.Precision Drawell provides best quality steel fibre .For more details,contact Precision Drawell.
ReplyDeletecool articcle bro
ReplyDeleteI think there is a small correction.
ReplyDeleteIn 2nd image for cantiliver beam. Replace clear cover with clear span.
In stress block diagram the Tension will pass through Center of the bar not from bottom edge of concrete.otherwise the information is very good.
IS there any poroblem regading myassignmenthelp fake ? nopes it is not true myassignmenthelp is the top company for assignment help
ReplyDeleteBrahmani Aluminium commenced its operations in the year 2005 and is among the prominent manufacturers, suppliers, and exporters of Aluminium Industrial Products and Components. The products offered by us are manufactured at par with the defined industry standards, so as to increase their demand in the global market. Considering the diversity of our range, our products are used across various industries, including construction, building, and others. Some of the pertinent features of our range include durability, shock resistance, leakproofness, and resistance to moisture.
ReplyDeleteAluminium Section Door Window Fabricator in ahmedabad
Aluminium Section Partition in ahmedabad
False Ceiling Work in ahmedabad
Upvc Door Window Manufacture in ahmedabad
I think this is an informative post and it is very useful and knowledgeable. therefore, I would like to thank you for the efforts you have made in writing this article.
ReplyDeletecomposition roofing contractor in Seattle
Awesome information!!! Thanks for providing it.
ReplyDeleteStorage And Warehouse Racks Suppliers In Qatar
| Shelving & Storage Equipment Supplies In Doha
| Racks And Shelves Doha | Racks And Shelves Doha
When I am alone, I come to see your comments. It is a very good comment, how strange is your loneliness in this city, there are thousands of people but no one is like that. One is changed because you are not there, yesterday even the sunlight did not come on the wall. Thank you from my heart.
ReplyDeleteCall Girls In Manesar
Call Girls Noida
Gurugram escort service
Call Girls Neemrana
Faridabad Escorts Service
call girls Sector 36
Gurugram Sector 39 Escorts
cheap escorts services in Gurugram
call girl sector 24
Sushant lok Escorts
Formaldehyde is a chemical molecule found in home items, building materials, and some consumer products, such as shampoo, as a preservative. Formaldehyde has been demonstrated to cause dermatitis and is known to cause contact allergies. It's also been known to aggravate allergic dermatitis and eczema in people who already have them. Parabens are chemical preservatives that have long been used to extend the shelf life of beauty products. Keep in mind that only half of the zydot ultra clean shampoo packet should be used initially, with the remaining half saved for after the purifier and before the conditioner. Since the natural accumulation of oil would expose the hair and scalp to recontamination throughout the day, Ultra Clean will remain effective for a period of 24 hours after usage. Visit: https://www.urineworld.com/
ReplyDeleteExcellent post. I was checking constantly this blog and I am impressed! Very helpful info specially the last part I care for such information a lot. I was looking for this certain info for a very long time. Thank you for sharing this.
ReplyDeleteTemporary Cooling Service UAE
Hello Dear
ReplyDeletePartial Safety Factor for Steel Material Is 1.15
Please check your stress graph of Steel
Thanks for your information! If you need Fashionable sunglasses so you can visit now My website.
ReplyDeleteThanks for sharing this great content, we really enjoyed the insign you bring to the topic, awesome stuff! Keep it up and share this kind of good knowledgeable content.
ReplyDeleteBridge and Structural Engineering
This explanation provides a detailed framework for designing a singly reinforced beam using the limit state method. If you need more detailed numerical examples or further clarification on any step, feel free to ask!
ReplyDeleteStruggling with management case studies and reports? Get professional support at Management Assignment Help and complete your work on time.
ReplyDelete